Note
Click here to download the full example code
SPGL1 Tutorial¶
In this tutorial we will explore the different solvers in the spgl1
package and apply them to different toy examples.
import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse.linalg import LinearOperator
from scipy.sparse import spdiags
import spgl1
# Initialize random number generators
np.random.seed(43273289)
Create random m-by-n encoding matrix and sparse vector
Solve the underdetermined LASSO problem for \(||\mathbf{x}||_1 <= \pi\):
b = A.dot(x0)
tau = np.pi
x, resid, grad, info = spgl1.spg_lasso(A, b, tau, verbosity=1)
print('%s%s%s' % ('-'*35, ' Solution ', '-'*35))
print('nonzeros(x) = %i, ||x||_1 = %12.6e, ||x||_1 - pi = %13.6e' %
(np.sum(np.abs(x) > 1e-5), np.linalg.norm(x, 1),
np.linalg.norm(x, 1)-np.pi))
print('%s' % ('-'*80))
Out:
================================================================================
SPGL1
================================================================================
No. rows : 50
No. columns : 128
Initial tau : 3.14e+00
Two-norm of b : 3.40e+00
Optimality tol : 1.00e-04
Target one-norm of x : 3.14e+00
Basis pursuit tol : 1.00e-06
Maximum iterations : 500
EXIT -- Optimal solution found
Products with A : 8 Total time (secs) : 0.0
Products with A^H : 8 Project time (secs) : 0.0
Newton iterations : 0 Mat-vec time (secs) : 0.0
Line search its : 0 Subspace iterations : 0
----------------------------------- Solution -----------------------------------
nonzeros(x) = 7, ||x||_1 = 3.141593e+00, ||x||_1 - pi = 0.000000e+00
--------------------------------------------------------------------------------
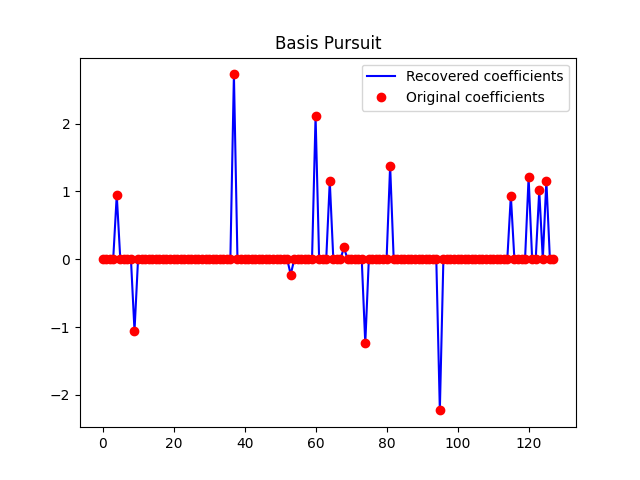
Solve the basis pursuit (BP) problem:
\[min. ||\mathbf{x}||_1 \quad subject \quad to \quad \mathbf{Ax} = \mathbf{b}\]
b = A.dot(x0)
x, resid, grad, info = spgl1.spg_bp(A, b, verbosity=2)
plt.figure()
plt.plot(x, 'b')
plt.plot(x0, 'ro')
plt.legend(('Recovered coefficients', 'Original coefficients'))
plt.title('Basis Pursuit')
plt.figure()
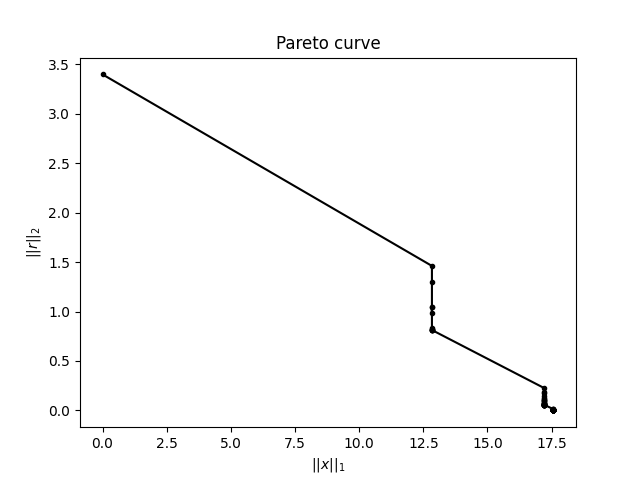
plt.plot(info['xnorm1'], info['rnorm2'], '.-k')
plt.xlabel(r'$||x||_1$')
plt.ylabel(r'$||r||_2$')
plt.title('Pareto curve')
plt.figure()
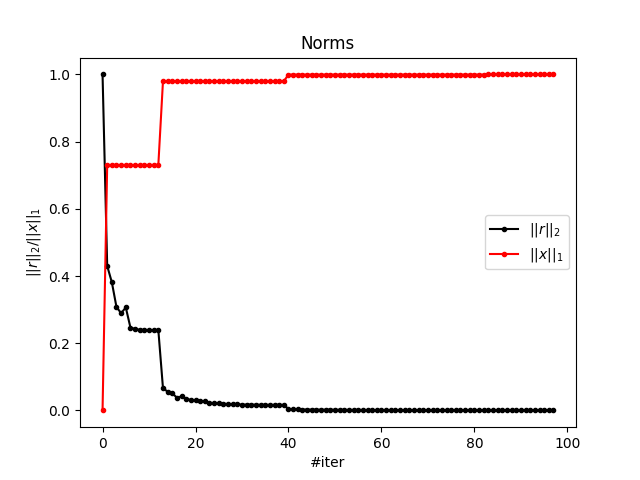
plt.plot(np.arange(info['niters']), info['rnorm2']/max(info['rnorm2']),
'.-k', label=r'$||r||_2$')
plt.plot(np.arange(info['niters']), info['xnorm1']/max(info['xnorm1']),
'.-r', label=r'$||x||_1$')
plt.xlabel(r'#iter')
plt.ylabel(r'$||r||_2/||x||_1$')
plt.title('Norms')
plt.legend()
Out:
================================================================================
SPGL1
================================================================================
No. rows : 50
No. columns : 128
Initial tau : 0.00e+00
Two-norm of b : 3.40e+00
Optimality tol : 1.00e-04
Target objective : 0.00e+00
Basis pursuit tol : 1.00e-06
Maximum iterations : 500
iterr Objective Relative Gap Rel Error gnorm stepg nnz_x nnz_g tau
0 3.3978494e+00 0.0000000e+00 1.00e+00 8.995e-01 0.0 0 0 1.2834830e+01
1 1.4610032e+00 1.6532743e+00 1.00e+00 3.459e-01 -0.6 67 1
2 1.2957367e+00 1.4480527e+00 1.00e+00 3.057e-01 0.0 53 1
3 1.0445582e+00 1.0186987e+00 1.00e+00 2.394e-01 0.0 33 1
4 9.8320803e-01 1.9671347e+00 9.83e-01 3.006e-01 0.0 17 1
5 1.0408537e+00 2.7237524e+00 1.00e+00 3.273e-01 0.0 15 1
6 8.3766484e-01 4.4627639e-01 8.38e-01 1.829e-01 0.0 20 1
7 8.2370803e-01 2.1784189e-01 8.24e-01 1.661e-01 0.0 16 1
8 8.1471442e-01 1.0576174e-01 8.15e-01 1.582e-01 0.0 15 1
9 8.1352564e-01 1.2833205e-01 8.14e-01 1.618e-01 0.0 12 2
10 8.1346284e-01 1.2136051e-01 8.13e-01 1.595e-01 0.0 12 3
12 8.1283336e-01 1.6431186e-03 8.13e-01 1.509e-01 0.0 12 12 1.7214207e+01
20 1.0262800e-01 3.7124664e-02 1.03e-01 1.684e-02 0.0 55 5
30 5.8775070e-02 2.1151854e-02 5.88e-02 9.905e-03 0.0 26 5
39 5.6081993e-02 3.4487799e-03 5.61e-02 9.059e-03 0.0 16 16 1.7561410e+01
40 1.3497461e-02 2.3368157e-02 1.35e-02 2.563e-03 0.0 61 17
50 6.5248570e-03 2.5729401e-02 6.52e-03 2.012e-03 -0.6 44 8
60 3.6779037e-03 8.0294188e-03 3.68e-03 8.458e-04 -0.9 30 30
70 1.7198692e-03 6.8520394e-04 1.72e-03 2.801e-04 0.0 17 17
80 1.3668596e-03 8.5588974e-05 1.37e-03 2.204e-04 0.0 14 14
82 1.3666459e-03 1.8193226e-05 1.37e-03 2.163e-04 0.0 14 14 1.7570044e+01
90 1.3860943e-04 4.2028246e-05 1.39e-04 2.222e-05 0.0 14 14
98 8.6425580e-05 5.4782377e-05 8.64e-05 1.545e-05 0.0 14 14
EXIT -- Found a root
Products with A : 131 Total time (secs) : 0.0
Products with A^H : 99 Project time (secs) : 0.0
Newton iterations : 4 Mat-vec time (secs) : 0.0
Line search its : 32 Subspace iterations : 0
<matplotlib.legend.Legend object at 0x7fdfcc084e48>
Solve the basis pursuit denoise (BPDN) problem:
b = A.dot(x0) + np.random.randn(m) * 0.075
sigma = 0.10 # Desired ||Ax - b||_2
x, resid, grad, info = spgl1.spg_bpdn(A, b, sigma, iter_lim=100, verbosity=2)
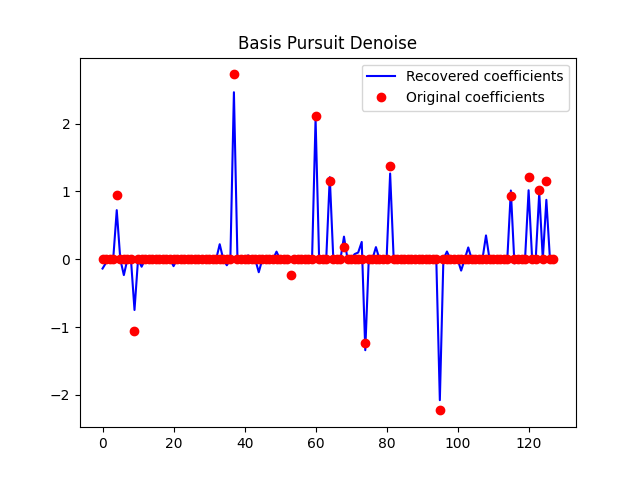
plt.figure()
plt.plot(x, 'b')
plt.plot(x0, 'ro')
plt.legend(('Recovered coefficients', 'Original coefficients'))
plt.title('Basis Pursuit Denoise')
Out:
================================================================================
SPGL1
================================================================================
No. rows : 50
No. columns : 128
Initial tau : 0.00e+00
Two-norm of b : 3.49e+00
Optimality tol : 1.00e-04
Target objective : 1.00e-01
Basis pursuit tol : 1.00e-06
Maximum iterations : 100
iterr Objective Relative Gap Rel Error gnorm stepg nnz_x nnz_g tau
0 3.4876525e+00 0.0000000e+00 9.71e-01 8.998e-01 0.0 0 0 1.3130733e+01
1 1.5278506e+00 1.5445083e+00 9.35e-01 3.512e-01 -0.6 70 1
2 1.3785367e+00 1.3210423e+00 9.27e-01 3.004e-01 0.0 48 1
3 1.1435885e+00 1.0754951e+00 9.13e-01 2.436e-01 0.0 36 1
4 1.0650070e+00 1.8808347e+00 9.06e-01 3.058e-01 0.0 24 1
5 1.1055544e+00 1.9676460e+00 9.10e-01 2.609e-01 0.0 14 1
6 9.7104698e-01 5.0757852e-01 8.71e-01 1.910e-01 0.0 21 1
7 9.5573059e-01 2.5393233e-01 8.56e-01 1.677e-01 0.0 20 1
8 9.5003110e-01 1.6053048e-01 8.50e-01 1.613e-01 0.0 19 1
9 9.4642238e-01 6.3958437e-02 8.46e-01 1.545e-01 0.0 16 1
10 9.4667260e-01 1.0342969e-01 8.47e-01 1.576e-01 0.0 15 1
12 9.4626463e-01 5.7319569e-03 8.46e-01 1.499e-01 0.0 15 15 1.8472152e+01
20 1.9419435e-01 4.1553930e-02 9.42e-02 2.642e-02 0.0 46 4 1.9164449e+01
30 1.0621175e-01 1.0890316e-02 6.21e-03 1.305e-02 0.0 48 38
40 1.0446001e-01 4.9732393e-03 4.46e-03 1.269e-02 0.0 47 47 1.9201152e+01
41 1.0004744e-01 1.2472217e-02 4.74e-05 1.237e-02 0.0 47 46
EXIT -- Found a root
Products with A : 53 Total time (secs) : 0.0
Products with A^H : 42 Project time (secs) : 0.0
Newton iterations : 4 Mat-vec time (secs) : 0.0
Line search its : 11 Subspace iterations : 0
Text(0.5, 1.0, 'Basis Pursuit Denoise')
Solve the basis pursuit (BP) problem in complex variables:
\[min. ||\mathbf{z}||_1 \quad subject \quad to \quad \mathbf{Az} = \mathbf{b}\]
class partialFourier(LinearOperator):
def __init__(self, idx, n):
self.idx = idx
self.n = n
self.shape = (len(idx), n)
self.dtype = np.complex128
def _matvec(self, x):
# % y = P(idx) * FFT(x)
z = np.fft.fft(x) / np.sqrt(n)
return z[idx]
def _rmatvec(self, x):
z = np.zeros(n, dtype=complex)
z[idx] = x
return np.fft.ifft(z) * np.sqrt(n)
# Create partial Fourier operator with rows idx
idx = np.random.permutation(n)
idx = idx[0:m]
opA = partialFourier(idx, n)
# Create sparse coefficients and b = A * z0
z0 = np.zeros(n, dtype=complex)
z0[p] = np.random.randn(k) + 1j * np.random.randn(k)
b = opA.matvec(z0)
# Solve problem
z, resid, grad, info = spgl1.spg_bp(opA, b, verbosity=2)
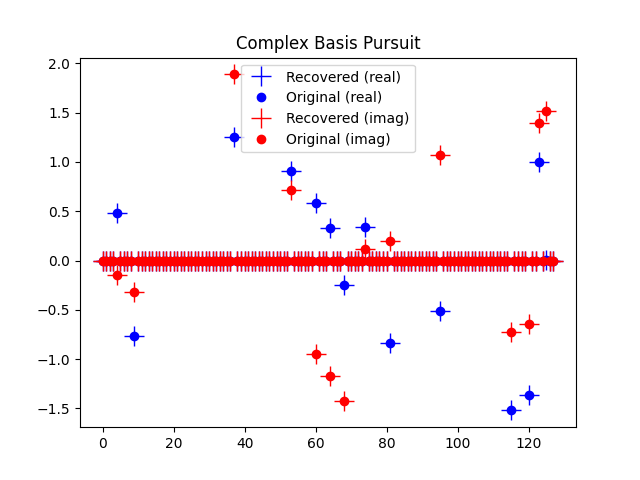
plt.figure()
plt.plot(z.real, 'b+', markersize=15.0)
plt.plot(z0.real, 'bo')
plt.plot(z.imag, 'r+', markersize=15.0)
plt.plot(z0.imag, 'ro')
plt.legend(('Recovered (real)', 'Original (real)',
'Recovered (imag)', 'Original (imag)'))
plt.title('Complex Basis Pursuit')
Out:
================================================================================
SPGL1
================================================================================
No. rows : 50
No. columns : 128
Initial tau : 0.00e+00
Two-norm of b : 3.23e+00
Optimality tol : 1.00e-04
Target objective : 0.00e+00
Basis pursuit tol : 1.00e-06
Maximum iterations : 500
iterr Objective Relative Gap Rel Error gnorm stepg nnz_x nnz_g tau
0 3.2278608e+00 0.0000000e+00 1.00e+00 9.900e-01 0.0 0 0 1.0524266e+01
1 1.7448418e+00 1.9165918e+00 1.00e+00 5.168e-01 -0.6 95 0
2 1.4600574e+00 1.5883031e+00 1.00e+00 3.875e-01 0.0 57 0
3 1.1700012e+00 7.2057823e-01 1.00e+00 2.294e-01 0.0 21 0
4 1.1387081e+00 6.0492162e-01 1.00e+00 2.591e-01 0.0 14 0
5 1.1192644e+00 6.3143375e-01 1.00e+00 2.339e-01 0.0 13 0
6 1.1110267e+00 2.5990247e-02 1.00e+00 1.887e-01 0.0 14 1
7 1.1109277e+00 1.8665102e-02 1.00e+00 1.882e-01 0.0 14 1
8 1.1109130e+00 9.8075649e-03 1.00e+00 1.876e-01 0.0 14 1 1.7103189e+01
9 4.0897300e-01 2.0290430e+00 4.09e-01 1.096e-01 0.0 33 0
10 2.4260476e-01 3.0388666e-01 2.43e-01 5.139e-02 0.0 84 0
20 7.3650715e-02 1.5598521e-01 7.37e-02 1.898e-02 -0.6 36 0
30 3.9788017e-02 1.6542009e-03 3.98e-02 6.363e-03 0.0 15 6
32 3.9782650e-02 1.1422412e-03 3.98e-02 6.356e-03 0.0 14 6 1.7352196e+01
40 5.2988820e-03 2.3780254e-03 5.30e-03 8.349e-04 0.0 45 37
50 1.0390591e-03 8.2222429e-04 1.04e-03 1.846e-04 0.0 14 14
60 4.3109396e-04 2.4523963e-04 4.31e-04 8.092e-05 0.0 14 14
65 4.2277734e-04 2.9843344e-06 4.23e-04 6.689e-05 0.0 14 14 1.7354868e+01
68 6.8724121e-05 5.4983919e-05 6.87e-05 1.067e-05 0.0 14 14
EXIT -- Found a root
Products with A : 85 Total time (secs) : 0.0
Products with A^H : 69 Project time (secs) : 0.0
Newton iterations : 4 Mat-vec time (secs) : 0.0
Line search its : 16 Subspace iterations : 0
Text(0.5, 1.0, 'Complex Basis Pursuit')
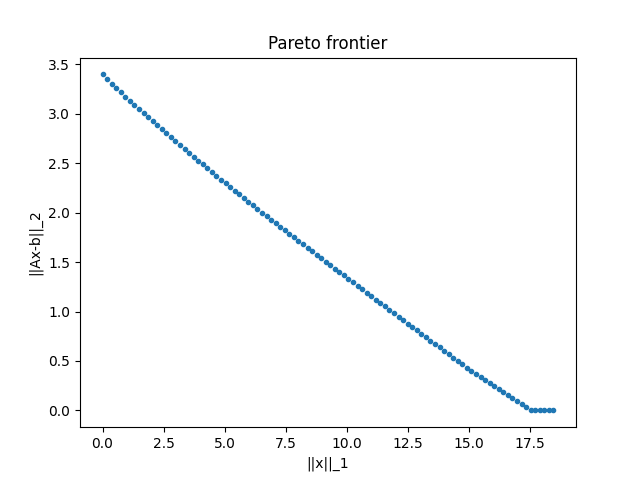
We can also sample the Pareto frontier at 100 points:
\[\phi(\tau) = min. ||\mathbf{Ax}-\mathbf{b}||_2 \quad subject \quad to \quad ||\mathbf{x}|| <= \tau\]
b = A.dot(x0)
x = np.zeros(n)
tau = np.linspace(0, 1.05 * np.linalg.norm(x0, 1), 100)
tau[0] = 1e-10
phi = np.zeros(tau.size)
for i in range(tau.size):
x, r, grad, info = spgl1.spgl1(A, b, tau[i], 0, x, iter_lim=1000)
phi[i] = np.linalg.norm(r)
plt.figure()
plt.plot(tau, phi, '.')
plt.title('Pareto frontier')
plt.xlabel('||x||_1')
plt.ylabel('||Ax-b||_2')
Out:
Text(42.722222222222214, 0.5, '||Ax-b||_2')
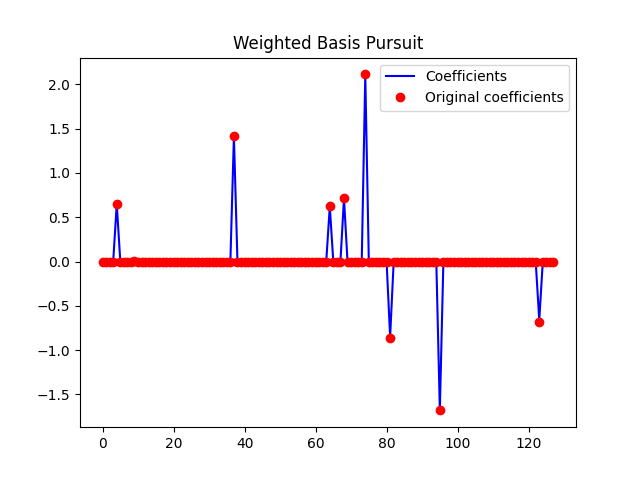
We now solve the weighted basis pursuit (BP) problem:
\[min. ||\mathbf{y}||_1 \quad subject \quad to \quad \mathbf{AW}^{-1}\mathbf{y} = \mathbf{b}\]
and
\[min. ||\mathbf{Wx}||_1 \quad subject \quad to \quad \mathbf{Ax} = \mathbf{b}\]
followed by setting :math`mathbf{y} = mathbf{Wx}`.
# Sparsify vector x0 a bit more to get exact recovery
k = 9
x0 = np.zeros(n)
x0[p[0:k]] = np.random.randn(k)
# Set up weights w and vector b
w = np.random.rand(n) + 0.1 # Weights
b = A.dot(x0 / w) # Signal
# Solve problem
x, resid, grad, info = spgl1.spg_bp(A, b, iter_lim=1000, weights=w)
# Reconstructed solution, with weighting
x1 = x * w
plt.figure()
plt.plot(x1, 'b')
plt.plot(x0, 'ro')
plt.legend(('Coefficients', 'Original coefficients'))
plt.title('Weighted Basis Pursuit')
k = 9
x0 = np.zeros(n)
x0[p[0:k]] = np.random.randn(k)
Finally we solve the multiple measurement vector (MMV) problem
\[min. | | \mathbf{Y} | |_{1, 2} \quad subject \quad to \quad \mathbf{AW}^{-1} \mathbf{Y} = \mathbf{B}\]
and the weighted MMV problem(weights on the rows of X):
\[min. | | \mathbf{WX} | |_{1, 2} \quad subject \quad to \quad \mathbf{AX} = \mathbf{B}\]
followed by setting \(\mathbf{Y} = \mathbf{WX}\).
# Create problem
m = 100
n = 150
k = 12
l = 6
A = np.random.randn(m, n)
p = np.random.permutation(n)[:k]
X0 = np.zeros((n, l))
X0[p, :] = np.random.randn(k, l)
weights = 3 * np.random.rand(n) + 0.1
W = 1/weights * np.eye(n)
B = A.dot(W).dot(X0)
# Solve unweighted version
x_uw, _, _, _ = spgl1.spg_mmv(A.dot(W), B, 0, verbosity=1)
# Solve weighted version
x_w, _, _, _ = spgl1.spg_mmv(A, B, 0, weights=weights, verbosity=2)
x_w = spdiags(weights, 0, n, n).dot(x_w)
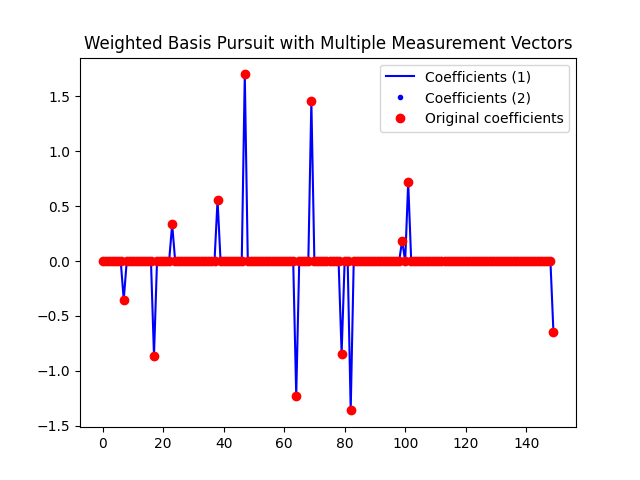
# Plot results
plt.figure()
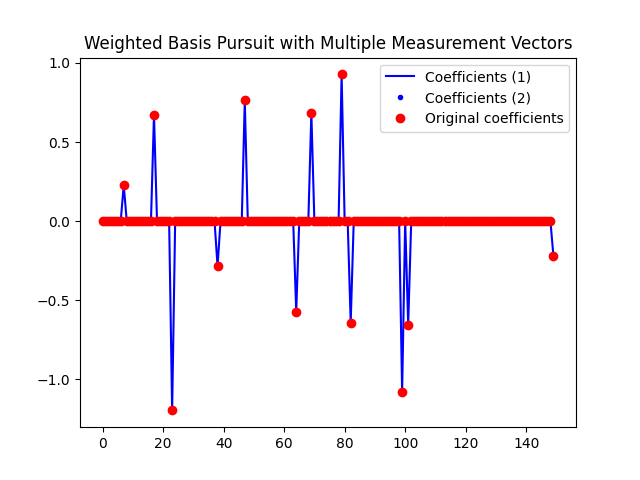
plt.plot(x_uw[:, 0], 'b-', label='Coefficients (1)')
plt.plot(x_w[:, 0], 'b.', label='Coefficients (2)')
plt.plot(X0[:, 0], 'ro', label='Original coefficients')
plt.legend()
plt.title('Weighted Basis Pursuit with Multiple Measurement Vectors')
plt.figure()
plt.plot(x_uw[:, 1], 'b-', label='Coefficients (1)')
plt.plot(x_w[:, 1], 'b.', label='Coefficients (2)')
plt.plot(X0[:, 1], 'ro', label='Original coefficients')
plt.legend()
plt.title('Weighted Basis Pursuit with Multiple Measurement Vectors')
Out:
================================================================================
SPGL1
================================================================================
No. rows : 600
No. columns : 900
Initial tau : 0.00e+00
Two-norm of b : 9.86e+01
Optimality tol : 1.00e-04
Target objective : 0.00e+00
Basis pursuit tol : 1.00e-06
Maximum iterations : 6000
/home/docs/checkouts/readthedocs.org/user_builds/spgl1/checkouts/latest/spgl1/spgl1.py:345: RuntimeWarning: invalid value encountered in true_divide
xc = xc / xa
EXIT -- Found a BP solution
Products with A : 4448 Total time (secs) : 2.6
Products with A^H : 2419 Project time (secs) : 1.8
Newton iterations : 14 Mat-vec time (secs) : 0.2
Line search its : 2029 Subspace iterations : 0
================================================================================
SPGL1
================================================================================
No. rows : 600
No. columns : 900
Initial tau : 0.00e+00
Two-norm of b : 9.86e+01
Optimality tol : 1.00e-04
Target objective : 0.00e+00
Basis pursuit tol : 1.00e-06
Maximum iterations : 6000
iterr Objective Relative Gap Rel Error gnorm stepg nnz_x nnz_g tau
0 9.8602912e+01 0.0000000e+00 1.00e+00 1.017e+03 0.0 0 0 9.5554864e+00
1 6.9417410e+01 1.9595302e+00 1.00e+00 6.916e+02 -0.6 419 0
2 5.1761792e+01 1.3643668e+00 1.00e+00 4.022e+02 0.0 212 0
3 4.4719199e+01 3.3088079e-01 1.00e+00 2.211e+02 0.0 96 0
4 4.4235054e+01 3.9317252e-01 1.00e+00 2.183e+02 0.0 89 0
5 4.4209620e+01 1.9011325e-01 1.00e+00 1.934e+02 0.0 88 0
6 4.4195524e+01 3.7232090e-03 1.00e+00 1.767e+02 0.0 95 0
7 4.4195175e+01 2.1356103e-03 1.00e+00 1.764e+02 0.0 95 0 2.0630352e+01
8 2.1170991e+01 7.4323046e+00 1.00e+00 1.091e+02 0.0 334 0
9 1.7331061e+01 2.2758703e+00 1.00e+00 5.633e+01 0.0 337 0
10 1.5859590e+01 3.6326634e+00 1.00e+00 5.650e+01 0.0 293 0
18 1.4217254e+01 4.3066544e-01 1.00e+00 3.173e+01 0.0 170 8 2.7000370e+01
20 5.5823227e+00 1.3015844e+01 1.00e+00 1.551e+01 0.0 646 0
30 2.4925735e+00 7.7271486e+00 1.00e+00 5.108e+00 0.0 196 4
34 2.4883824e+00 7.4225525e-01 1.00e+00 4.266e+00 0.0 188 11 2.8451690e+01
40 4.1105039e-01 5.9696329e+01 4.11e-01 2.529e+00 0.0 316 0
50 1.0902142e-01 1.6349931e+00 1.09e-01 1.801e-01 0.0 137 4
60 4.9748935e-02 1.8398584e+00 4.97e-02 1.471e-01 0.0 72 2
63 4.9435528e-02 3.6531447e-02 4.94e-02 8.404e-02 0.0 72 12 2.8480769e+01
70 1.1780283e-02 5.0958811e+00 1.18e-02 1.780e-01 0.0 72 0
80 1.5540978e-03 4.8472422e-02 1.55e-03 3.408e-03 0.0 72 4
90 6.7461437e-04 7.6278843e-03 6.75e-04 1.402e-03 0.0 72 34
95 6.7316524e-04 1.4549718e-03 6.73e-04 1.180e-03 0.0 72 57 2.8481154e+01
100 1.8442074e-04 9.0788110e-03 1.84e-04 5.075e-04 0.0 72 72
103 9.4798950e-05 6.5696437e-03 9.48e-05 3.365e-04 0.0 72 72
EXIT -- Found a BP solution
Products with A : 114 Total time (secs) : 0.1
Products with A^H : 104 Project time (secs) : 0.0
Newton iterations : 6 Mat-vec time (secs) : 0.0
Line search its : 10 Subspace iterations : 0
Text(0.5, 1.0, 'Weighted Basis Pursuit with Multiple Measurement Vectors')
Total running time of the script: ( 0 minutes 4.441 seconds)